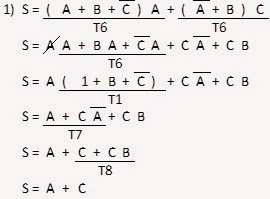• Algebra de boole
• Mapas de karnaugh
• Circuitos de
conmutación
• Compuertas
lógicas
• Pasos para
diseñar circuitos digitales
• Ejemplo de
diseño según los pasos
ÁLGEBRA DE BOOLE
El álgebra de Boole es toda
clase o conjunto de elementos que pueden tomar dos valores perfectamente
diferenciados, que se definen por "0" y "1" y que están
relacionados por las operaciones binarias de suma (+) y producto (.) lógicos
que cumplen diferentes teoremas y postulados:
TEOREMAS Y POSTULADOS DEL
ÁLGEBRA DE BOOLE :
La estructura
del álgebra de Boole se fundamenta en los teoremas:
Según el
álgebra de Boole se establece matemáticamente:
Ejemplo.
Las
siguientes funciones han sido resueltas utilizando el álgebra de Boole,
paso a paso indicando que teorema fue empleado en cada paso.
MAPAS DE KARNAUGH
Un mapa de
Karnaugh es un diagrama utilizado para la simplificación de funciones
algebraicas Booleanas.
Los mapas de
Karnaugh reducen la necesidad de hacer cálculos extensos para la simplificación
de expresiones booleanas, permitiendo así identificar y eliminar
condiciones muy inmensas.
La tabla de
verdad de una función de N variables posee 2N filas, el mapa Karnaugh
correspondiente debe poseer también 2N cuadrados. Las variables
de la expresión son ordenadas en función de su peso y siguiendo el código
Gray, de manera que sólo una de las variables varía entre celdas adyacentes. La
transferencia de los términos de la tabla de verdad al mapa de Karnaugh se
realiza de forma directa, albergando un 0 ó un 1, dependiendo del valor que
toma la función en cada fila. Es recomendable usar el mapa de Karnaugh para
funciones de hasta 5 variables.
Mapa de
karnaugh para 2 variables
Mapa de
karnaugh para 3 variables
Mapa de
karnaugh para 4 variables
Mapa de
karnaugh para 5 variables
Ejemplo.
1) f
(A,B,C) = Ʃm (0 , 1 , 3 , 4 , 5 , 7) = πM (
2 , 6)
2) f
(A,B,C) = Ʃm (0 , 2 , 3 , 5 , 7) = πM (
1 , 4 , 6)
3) f
(A,B,C,D) = Ʃm (0 , 1 , 2 , 13 , 15)
4) f
(A,B,C,D,E) = Ʃm (0 , 1 , 2 , 13 , 15 ,
30 , 31)
CIRCUITOS DE
CONMUTACIÓN
Formados por compuertas que implementan las
operaciones logicas (and,or y not)
Señales eléctricas y valores lógicos las tablas se
definen con:
- Voltaje alto H
- Voltaje bajo L
El
diseñador decide:
Lógica positiva 1
-> H Lógica negativa 1 -> L
0 -> L 0 -> H
Niveles
Logicos
Vcc = 5v
VOH min = 2,7v -> High state DC noise margin
VOH
min = 2,0v
VIL max =
0,8v -> Low state DC noise
margin
VOL max =
0,5v
COMPUERTAS LÓGICAS
Compuertas
Básicas
Compuertas Adicionales
Pasos
para resolver problemas:
1) Leer bien (entender)
2) Definir variables de in/out
3) Realizar tabla de verdad
4) Determinar función de salida
5) Minimizar y determinar nueva función
6) Implementar diseño y probar
7) Montar circuito
Ejemplo.
Alarma para
Se desea construir una alarma para detectar si falla o deja de funcionar un semáforo de transito, el problema se resolverá siguiendo los pasos mencionados anteriormente.
1) Leer bien (entender)
El enunciado nos dice que hay 3
entradas y una salida que sera 1 lógico cuando, todas las entradas sean 0 lógico o cuando 2 o mas entradas sean 1 lógico, se empleara lógica positiva.
2) Definir variables de entrada y salida
3) Realizar tabla de verdad
4) Determinar función de salida
5) Minimizar y determinar nueva función
6) Implementar diseño y probar
7) Montar circuito
Para montar el circuito se requiere:
- un
protoboard,
- 3 resistencias de 330Ω,
- 3 LED (para verificar las señales in/out),
- IC 7408
- IC 7432
- cable UTP
- una fuente de 5 volt
- alicate (para cortar el cable a
medida)